ডপলার ইফেক্টের মানে কিছুটা হলেও বোঝা গেল। এবার আমরা একটু বেশি বিস্তারিত খুঁটিয়ে দেখব।
আসলে ডপলার ইফেক্ট হয় আপেক্ষিক বেগের জন্য। তরঙ্গের সোর্স আর সেই তরঙ্গের অবজারভার — এদুটোর আপেক্ষিক বেগ থাকলে অবজারভার সেই তরঙ্গকে ভিন্ন তরঙ্গদৈর্ঘ্যে বা কম্পাংকে পাবে। এটাই আসলে ডপলার ইফেক্ট।
অবজারভার কোনোদিনই আসল তরঙ্গদৈর্ঘ্য বা কম্পাংক পাবে না, যদি আপেক্ষিক বেগ থাকে, মানে ডপলার ইফেক্ট হয়।
তাহলে কীভাবে পাবে, মানে অবজারভার কত তরঙ্গদৈর্ঘ্যের বা কত কম্পাংকের তরঙ্গ পাবে, সেটাই হচ্ছে ডপলার ইফেক্টের মূল সমীকরণগুলোর মজা।
৫.
শব্দকে আমরা ডপলার ইফেক্ট ব্যাখ্যা করার জন্য নিতে পারি। ট্রেন যখন হুইসেল বাজাতে বাজাতে কাছে আসে, তখন কেন মনে হয় যে হুইসেলের শব্দ তীব্র হচ্ছে? আর কেনই বা দূরে সরে যেতে থাকলে শব্দ মৃদু হয়ে যাচ্ছে? ট্রেন তো সবসময় একই কম্পাংকের হুইসেল দিচ্ছে! তাহলে কেমনে কী?
আসল কারণ একটাই, কম্পাংকের পরিবর্তন।
এখানে ট্রেন হচ্ছে তরঙ্গের সোর্স।
সোর্স তরঙ্গ ছাড়তে ছাড়তে চলে যাচ্ছে। অবজারভার আমরা, ট্রেন লাইনের পাশে। আমরা স্থির৷ আমরা সেই তরঙ্গকে ভিন্ন কম্পাংকে বা ফ্রিকুয়েন্সিতে পাচ্ছি।
আবার আমরা যখন দৌড়ে কোনো স্থির সোর্সের কাছে যাবো, তখন শব্দ তীব্র হতে থাকে, আবার দূরে দৌড়ে যেতে থাকলে মৃদু হতে থাকে। অথচ সোর্স সবসময় একই কম্পাংকের শব্দ করছে। তাহলে কেন আমরা এমন পাই?
কারণ সোর্স আর আমরা অবজারভারদের মাঝে আপেক্ষিক গতি আছে।
আবার যদি সোর্স আর অবজারভার দুটোই একইসাথে গতিশীল হয়, তাহলে?
তখনও অবজারভারের কাছে তরঙ্গের পরিবর্তন হবে।
এখানে আমরা তিন টাইপের অবস্থা দেখলাম। ক্ল্যাসিক্যাল মেকানিক্সে ডপলার ইফেক্ট উপরের এই তিন টাইপের হতে পারে,
১. সোর্স স্থির, অবজারভার মুভ করছে,
২. সোর্স মুভ করছে অবজারভার স্থির,
৩. অবজারভার আর সোর্স দুটোই মুভ করছে।
এবার একটু বুঝতে চেষ্টা করি, কেন এই তিনটে পয়েন্টে আমরা এরকম পাই। তারপর আমরা সমীকরণ থেকে বের করে গোপন কিছু কথা উদ্ধার করব, কেমন?
৬.
টাইপ-১:
সোর্স স্থির, অবজারভার মুভ করছে।
আমরা প্রথমে একটা ফাঁকা রাস্তা কল্পনা করি৷ একদম ফাঁকা, কেউ নেই। শুধু সোর্স হিসেবে একটা গাড়ি, আর অবজারভার হিসেবে আমরা।
আমরা স্থির, গাড়িও স্থির। এমন অবস্থায় গাড়ি থেকে শব্দ বের হওয়া শুরু হলো। শব্দ আপন মনে গাড়ির সামনে, পেছনে, ডানে, বামে, উপরে — ছড়িয়ে পড়ছে। অনেকটা শান্ত পানিতে ছোয়া দিলে যেমন হয় আরকি। এই শব্দের বেগ হচ্ছে vᵥᵥ (মনে রাখার টেনশন করবেন না, v মানে বেগ, আর নিচের vv মানে wave বা তরঙ্গ। মানে মূল শব্দ তরঙ্গের বেগ।)
আমরা এখনো স্থির, সোর্সও এখনও স্থির৷ এমন অবস্থায় আমরা কী শব্দের আসল কম্পাংক শুনতে পাবো? অবশ্যই পাবো। আমাদের দুটোর (মানে সোর্স আর অবজারভার) মাঝে কোনো আপেক্ষিক বেগ নেই।
ব্যাস, খেলা শেষ।
৭.
এবার আসল কেসে আসি।
টাইপ-১ এ আমরা মুভ করছি, সোর্স স্থির। খেয়াল করুন, আমরা দুই দিকে দৌড়াতে পারি।
১. শব্দের গতির দিকে, মানে শব্দ তরঙ্গের মুখোমুখি,
২. শব্দের সাথে একই দিকে, মানে শব্দের সাথে দৌড় পাল্লা দিয়ে।
চলুন, আগে এক নম্বর কন্ডিশনে আমরা দেখি৷
কল্পনা করুন, আমরা সোর্সের দিকে দৌড়ে যাচ্ছি। শব্দ তো আবার আমাদের দিকেই ধেয়ে আসছে, কারণ ওইযে, শব্দ গাড়ির সবদিক দিয়েই সামনে এগিয়ে যাচ্ছে। আমরা গাড়ির দিকে যাচ্ছি vₒ বেগে (o মানে অবজারভার)। মানে শব্দ আর আমাদের গতি পরস্পরের বিপরীত দিকে!
তার মানে আমরা শব্দের বেগকে কত দেখব? ধরি আমরা বেগ মাপলাম। আর আমাদের বেগ vₒ = 2 m/s ।
Vᵥᵥ = 4 m/s হলে আমাদের মাপা শব্দের বেগ আর এই বেগ কি সমান?
কখনোই না৷ কারণ আমরাও তো শব্দের বেগের বিপরীতে দৌড়েচ্ছি। মানে আমরা আর শব্দ মুখোমুখি আসছি। তাহলে শব্দ তরঙ্গ যদি এক সেকেন্ডে আমাদের দিকে 4 m অগ্রসর হয়, তাহলে আমরা এই 1 সেকেন্ডে যদি 2 মিটার সামনে এগিয়ে যাই তাহলে আমরা এই 1 সেকেন্ড পর শব্দকে কত কাছে পাবো?
নিশ্চই 4+2 = 6 মিটার!
তার মানে আমরা 1 সেকেন্ডে শব্দকে কাছে পাচ্ছি 6 মিটার করে। 2 সেকেন্ডে পাচ্ছি 6 × 2 = 12 মিটার কাছে, 3 সেকেন্ডে 18, 4 সেকেন্ডে 24 — এইযে 6 মিটার করে কাছে আসছে, এটা কিন্তু আমাদের দেখতে পাওয়া শব্দের বেগ! আমাদের নিজেদের সাপেক্ষে তো আমরা স্থিরই। তাহলে আমরা অবজারভারেরা শব্দের বেগ পাচ্ছি vᵥᵥ + vₒ । এটা হচ্ছে শব্দ আর অবজারভারের মধ্যেকার আপেক্ষিক বেগ।
তাহলে এখন আমরা শব্দের বেগ দেখতে পাচ্ছি আসল শব্দের বেগ থেকে বেশি। আবার, খেয়াল করলে দেখবেন, তরঙ্গের বেগ, v = fλ,
f হচ্ছে কম্পাংক বা ফ্রিকুয়ান্সি, আর λ হচ্ছে তরঙ্গদৈর্ঘ্য।
মানে v যদি চেঞ্জ হয়, তাহলে শিওর f বা λ এর যেকোনো একটি বা দুটিই চেঞ্জ হয়েছে। বেড়েছে বা কমেছে।
৮.
এখন এখানে বাড়লোটা কে??
“আয়রনম্যান প্রচণ্ড দ্রুত দৌড়ে যাচ্ছে… আয়রনম্যানের দিকে লক্ষ্য করে অনবরত ফায়ারিং হচ্ছে… এক লাইনে বুলেটগুলো আসছে… আয়রনম্যান দাঁড়িয়ে পড়লো… প্রতি সেকেন্ডে পাঁচটা করে বুলেট শরীরে এসে লাগছে… না, থামলে হবে না দৌড়ানো আবার শুরু হলো… এবার দেখা গেল যে প্রতি সেকেন্ডে ৮ টা বুলেট গায়ে লাগছে…! দৌড়ানোর জন্য দুটো বুলেটের মাঝে যে গ্যাপ, সেই গ্যাপের খানিকটা আয়রনম্যান অতিক্রম করছে… যার ফলে আয়রনম্যানের কাছে দুটো বুলেটের মাঝের দূরত্ব কমে এসেছে …. — খবর — ”
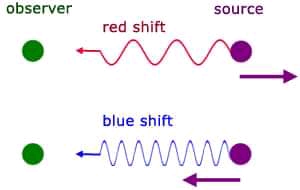
প্রতি সেকেন্ডে যতটা তরঙ্গদৈর্ঘ্য যায়, সেটা হচ্ছে কম্পাংক। চিত্রের প্রত্যেক ‘))’ হচ্ছে একটা করে তরঙ্গদৈর্ঘ্যের সমান দূরত্ব। ‘)))’ মানে দুই তরঙ্গদৈর্ঘ্যে দূরত্ব। ‘))))’ হচ্ছে তিন তরঙ্গদৈর্ঘ্য।
একটা ‘)’ হচ্ছে তরঙ্গের একটা চূড়া। আর তার পরের ‘)’ দিয়ে বুঝায় যে আরেকটা চূড়া, একই দশার। মোটাদাগে ‘))’ মানে দুটো চূড়া, দুটো চূড়া নিয়ে এক তরঙ্গদৈর্ঘ্য। এরকম এক সেকেন্ডে যতটা ‘)’ দেখতে পাবো বা অব্জার্ভ করতে পারব, সেটা হচ্ছে তরঙ্গটার কম্পাংক বা ফ্রিকুয়েন্সি।
তো আমরা যখন স্থির ছিলাম, প্রতি সেকেন্ডে একটা নির্দিষ্ট ‘)’ এসে কানে ধরা দিতো। আর দুইটা ‘)’ এর মাঝে যে দূরত্ব, সেটা কিন্তু শুধুমাত্র শব্দের নিজস্ব বেগ দিয়েই অতিক্রান্ত হতো।
যখন শব্দের বেগের মুখোমুখি দৌড় দিচ্ছি, তখন কিন্তু দুইটা ‘)’ এর মধ্যে দুরত্ব শুধু শব্দের বেগ অতিক্রম করছে না! আমাদের বেগও ভাগ রেখেছে।
কীভাবে?
ধরা যাক দুটো ‘)’ বা চূড়ার মাঝের দূরত্ব অতিক্রম করতে শব্দের বেগের জন্য 3 সেকেন্ড লাগে। তাহলে দেখুন, ‘))’ এর ডান দিকের ‘)’ যখন আমাদের কানে পৌছালো, তখন আমরা দৌড়াচ্ছি। এখন বামদিকের ‘)’ শব্দের বেগে কানে পৌছাতে যেন কত সময় লাগবে? হ্যাঁ, 3 সেকেন্ড। তাহলে দেখুন, 1 সেকেন্ড পরও ওই চূড়াটা কানে পৌছায়নি। পৌছাতে 3 সেকেন্ড লাগার কথা। কিন্তু দেখুন, আমরাও কিন্তু নিজস্ব বেগের জন্য এই 1 সেকেন্ড সময়ে শব্দের মুখোমুখি কিছুটা এগোচ্ছি!
এই কিছুটা এগোনোটা কিন্তু ঠিকই ওই দুই চূড়া মানে ‘))’ এর মাঝের কিছু দূরত্বটাই অতিক্রম করে ফেলছি! মানে আমরা 3 সেকেন্ডের কম সময়েই ‘))’ এর বামের চূড়াটা কানে ধরে ফেলবো!
তার মানে যেন কী?
হ্যাঁ, কম সময়ে এক তরঙ্গদৈর্ঘ্য দূরত্ব অতিক্রম করতে দেখব। তাহলে কম সময়ে এক তরঙ্গদৈর্ঘ্য অতিক্রম করতে দেখলে 1 সেকেন্ডে নিশ্চই আগের চেয়ে বেশি চূড়া বা ‘)’ কানে পৌছাচ্ছে! কিন্তু 1 সেকেন্ডে যতটা চূড়া কানে পৌছায়, সেটা তো আর কেউ নয়, সেটাই তো কম্পাংক!
মানে এই বেড়ে যাওয়া বাচ্চাটা কম্পাংক বা ফ্রিকুয়ান্সি।
তরঙ্গদৈর্ঘ্যটা কিন্তু এখানে ঠিকই আছে, মাথায় রাখতে হবে। কম্পাংক বেড়েছে। একটা তরঙ্গের ছবি চিন্তা করুন। তরঙ্গটা চলছে। এখন তরঙ্গটার বেগ বাড়িয়ে দিন। কী, তরঙ্গদৈর্ঘ্য চেঞ্জ হলো? না। চেঞ্জ হয়েছে শুধু চূড়াগুলো ওঠানামার হার।
বেগ বাড়িয়ে দেওয়ায় এক তরঙ্গদৈর্ঘ্য অতিক্রম করার সময়টা কমে যাচ্ছে। তাই কম্পাংক বাড়ছে।
তরঙ্গদৈর্ঘ্যে পরিবর্তন আসছে না।
তরঙ্গদৈর্ঘ্যটা তখনই চেঞ্জ হবে, যখন সোর্স নিজেই মুভ করবে। কারণ তখন সোর্স ফার্স্ট চুড়া ছাড়ার পর কিছুটা দুরত্বে এগিয়ে গিয়ে সেকেন্ড চূড়াটা ছেড়ে এক তরঙ্গদৈর্ঘ্য পুরো করবে। এইযে সোর্স কিছুটা এগিয়ে গেল, এর জন্য দুইটা কন্ডিশনে তরঙ্গদৈর্ঘ্য কমতে বা বাড়তে পারে। সেটার আলোচনা টাইপ-২ দেখার সময় দেখা যাবে।
৯.
তো আমরা আবার আগের চিন্তায় ফিরে যাই।
আমাদের জন্য শব্দের বেগ,
vᵥᵥ + vₒ,
আর তরঙ্গদৈর্ঘ্য সবসময় সমানই থাকলো, বেড়ে গেল কম্পাংক।
তো এখন আমরা এইযে বেড়ে গেল যে, সেই বেড়ে গিয়ে কম্পাংক কত হলো, সেটা নির্ণয় করতে চেষ্টা করব। বেশ মজার জিনিস।
আমরা জানি, v = fλ সকল তরঙ্গের জন্য সত্যি।
এখন তরঙ্গের আসল কম্পাংক, যেটা সোর্স থেকে এসেছে fᵥᵥ আর আমরা অবজারভারেরা যে কম্পাংক পাচ্ছি, সেটা হচ্ছে fₒ ।
আর তরঙ্গদৈর্ঘ্য তো সবসময়ই λᵥᵥ ।
তো, vᵥᵥ + vₒ হচ্ছে অবজারভারের সাপেক্ষে তরঙ্গের বেগ, আর λᵥᵥ হচ্ছে তরঙ্গদৈর্ঘ্য।
তাই, বেগ = কম্পাংক × তরঙ্গদৈর্ঘ্য
বা, vᵥᵥ + vₒ = fₒλᵥᵥ ….. (1)
আবার, সোর্সের থেকে আসা আসল বেগ, কম্পাংক আর তরঙ্গদৈর্ঘ্যের সম্পর্ক,
vᵥᵥ = fᵥᵥλᵥᵥ
বা, λᵥᵥ = vᵥᵥ/fᵥᵥ ….. (2)
এবার (1) আর (2) থেকে লিখতে পারি,
vᵥᵥ + vₒ = fₒvᵥᵥ/fᵥᵥ
বা, fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/vᵥᵥ]
তার মানে আমরা যে কম্পাংক দেখতে পাবো, সেটা জানতে মূল কম্পাংকের সাথে (vᵥᵥ + vₒ)/vᵥᵥ গুণ দিলেই হলো, তাই না?
হ্যাঁ, মজাটা এখানেই।
(vᵥᵥ + vₒ)/vᵥᵥ কিন্তু সবসময়ই 1 এর চেয়ে বড়ো।
কারণ (vᵥᵥ + vₒ) তো এমনিতেই vᵥᵥ থেকে বড়ো, আর যখন এই বড়ো সংখ্যাকে vᵥᵥ, তুলনামূলক ছোটো সংখ্যা দিয়ে ভাগ দেওয়া হয়, তখন তো ভাগফল 1 এর চেয়ে বড়োই হবে। তাহলে fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/vᵥᵥ] তে নিশ্চই fᵥᵥ এর চেয়ে fₒ বড়ো হবে। মানে আমরা অব্জার্ভ করা কম্পাংক বেশি পাবো। বেশি তীব্র শব্দ শুনতে পাবো।
তবে আরেকটু বেশি মজার ব্যাপার হলো, আমরা এখনও সেকেন্ড কন্ডিশনে, যেখানে শব্দের বেগের সাথে পাল্লা দিয়ে দৌড়াবো — সেটা নিয়ে কোনো কথা না বলেই সমীকরণ বলে দিতে পারি!
কিন্তু কীভাবে?
খেয়াল করুন, যখন শব্দের বেগের সাথে পাল্লা দিচ্ছি, তখন আপেক্ষিক বেগটা হবে (vᵥᵥ – vₒ), কারণ এখানে আমরা শব্দের বেগকে কম দেখব৷
আগের মতোই ধরি 4 m/s শব্দের বেগ। আমরা পাল্লা দিচ্ছি 2 m/s বেগে। তাহলে, শব্দ যাচ্ছে 1 সেকেন্ডে 4 মিটার। আমরা পাল্লা দিয়ে এগোচ্ছি 1 সেকেন্ডে 2 মিটার। তাহলে শব্দের চেয়ে প্রতি 1 সেকেন্ডে পিছিয়ে থাকব কত মিটার করে? নিশ্চই 4 – 2 = 2 মিটার করে! তাহলে বেগ কত, ১ সেকেন্ডে 2 মিটার করে শব্দের চেয়ে পিছিয়ে যেতে থাকলে বেগ হবে 2 m/s ।
যার অর্থ বেগ পাচ্ছি, (vᵥᵥ – vₒ) ।
এখন আগের মতো সমীকরণ তুলে বের করেই দেওয়া যায়, এটার কম্পাংক,
fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/vᵥᵥ]
পার্থক্য শুধু শব্দের বেগ আর অবজারভারের বেগের বিয়োগফল, আগে ছিল যোগফল৷ এটাতে দেখলে দেখা যাবে যে fᵥᵥ এর চেয়ে fₒ ছোটো। মানে আমরা অব্জার্ভ করা কম্পাংক কম পাচ্ছি বা শব্দের তীব্রতা হারাতে দেখব।
১০.
তো আমরা টাইপ-১ এর জন্য সমন্বিত সমীকরণ লিখতেই পারি।
যখন শব্দের বেগের বিপরীতে যাচ্ছি তখন,
fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/vᵥᵥ]
যখন একই সাথে পাল্লা দিচ্ছি তখন,
fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/vᵥᵥ]
একসাথে লিখলে,
fₒ = fᵥᵥ [(vᵥᵥ ± vₒ)/vᵥᵥ]
প্লাস নেব যখন অবজারভার শব্দের বিপরীতে যাচ্ছে,
মাইনাস নেব যখন অবজারভার শব্দের দিকে যাচ্ছে।
শেষ।
এখন একটা প্রশ্ন,
আচ্ছা, এখানে সব সমীকরণ আমরা এই ভেবে এনেছি যে আমরা শব্দের কম বেগে মুভ করব।
কেননা (vᵥᵥ – vₒ) সর্বদা ধনাত্মক, কারণ এটাকে লেখা যায়, vᵥᵥ – vₒ = fₒλᵥᵥ যেখানে fₒ আর λᵥᵥ সবসময় ধনাত্মক। তাহলে বামপক্ষ (vᵥᵥ – vₒ) কে সবসময় ধনাত্মকই হতে হচ্ছে! মানে vᵥᵥ বা শব্দের বেগকে সবসময় বড়ো ধরা হচ্ছে।
কিন্তু সুপারসনিক প্লেন তো শব্দের চেয়েও দ্রুত বেগে চলে! তখন কেমন করে হবে ডপলার ইফেক্ট? কেমন করে?
ভাবুন, ভালো করে ভাবুন। কোথাও কিছু মিস যাচ্ছে কিনা খুঁটিয়ে দেখতে হবে…!
১১.
আগের পর্বে আমরা টাইপ-১ মানে অবজারভারের বেগের জন্য ডপলার ইফেক্ট দেখেছি। শুধু কম্পাংক পরিবর্তন হতো। এবার দেখব টাইপ-২, এটাতে সোর্স নিজেই মুভ করবে। আর মজার ব্যাপার হচ্ছে এটাতে তরঙ্গদৈর্ঘ্যের পরিবর্তন হবে!
তো চলুন, শুরু করা যাক।
টাইপ-২:
সোর্স মুভ করছে, অবজারভার স্থির।
আগের অবস্থায় ফিরে যাই। সোর্স আর অবজারভার — দুটোই স্থির, ফাঁকা রাস্তা, ঠান্ডা হাওয়া আসছে… অংক করার জন্য সর্বোত্তম পরিবেশ।
সোর্স হঠাৎ চলতে শুরু করলো, শব্দ ছাড়তে ছাড়তে যাচ্ছে। কোনদিকে যাবে?
দুইদিক হতে পারবে সর্বোচ্চ।
১. আমাদের দিকে আসছে,
২. আমাদের থেকে দূরে সরে যাচ্ছে।
প্রথম কন্ডিশন চিন্তা করি।
সোর্সকে আবার স্থির ধরে নিলাম।
আমরাও স্থির৷ একই শান্ত পরিবেশ, ঠান্ডা হাওয়া আসছে…!
সোর্স থেকে শব্দের তরঙ্গের একটা চূড়া বের হলো। নির্দিষ্ট সময় পর আরেকটা চূড়া বের হয়ে 1 তরঙ্গদৈর্ঘ্য পুরো করবে। মানে ‘))’ পাবো। এই নির্দিষ্ট সময়টা কী?
এটা কি কম্পাংক? না।
এটা হচ্ছে পর্যায়কাল।
মনে রাখতে হবে, কম্পাংক হচ্ছে প্রতি সেকেন্ডে কয় তরঙ্গদৈর্ঘ্য অতিক্রম করা হয়েছে, সেটা।
আর পর্যায়কাল হচ্ছে 1 তরঙ্গদৈর্ঘ্য অতিক্রম করার জন্য যত সময় লাগে সেটা।
দেখুন,
1 তরঙ্গদৈর্ঘ্য অতিক্রম করতে লাগে T সময় (পর্যায়কাল)
বা, T সেকেন্ড সময়ে অতিক্রান্ত হয় 1 তরঙ্গদৈর্ঘ্য
বা, 1 সেকেন্ডে অতিক্রান্ত হয় 1/T তরঙ্গদৈর্ঘ্য! (এটা হচ্ছে কম্পাংক, খেয়াল করুন।)
মানে কম্পাংক আর পর্যায়কালের সম্পর্ক হচ্ছে,
f = 1/T ।
তো সেই নির্দিষ্ট সময় মানে 1 পর্যায়কাল পরেই কিন্তু সোর্স থেকে দ্বিতীয় চূড়াটা বের হয়ে 1 তরঙ্গদৈর্ঘ্য পুরো করবে। এখানে সোর্সের নিজের গতি নেই৷ ব্যাস, ডপলার ইফেক্ট খাটবে না৷
১২.
স্থির অবস্থা থেকে সোর্স গতিশীল হলো।
এখন সোর্সের বেগ আছে, vₛ । তরঙ্গের বেগ তো আছেই, vᵥᵥ । অবজারভার মানে আমরা স্থির।
সোর্স আমাদের কাছে আসছে।
আমরা শব্দের বেগ কত পাব?
সোর্স আর শব্দ তো একইদিকে, মানে আমাদের দিকে আসছে। তাহলে বেগ কত হবে শব্দের?
নিশ্চই (vᵥᵥ – vₛ) m/s ?
না, ভুল।
কেন ভুল?
দেখুন, সোর্স শব্দ ছাড়তে ছাড়তে আসছে। সোর্সের উপরে বসে বসে আসছে না!
সোর্স শব্দ বাতাসে ছেড়ে দিচ্ছে, বাতাসে শব্দ নিজের বেগে চলে আমাদের কাছে আসছে। মানে কী দাঁড়ালো?
সোর্স বাতাসে বা আর কোনো মাধ্যম হোক, শব্দ তরঙ্গ ছেড়ে দেওয়ার পর শব্দ নিজের মাধ্যমেই নিজের গতিতেই চলবে। শব্দ ছাড়লো, তো সোর্সকে দেখার টাইম নেই। সোর্স শব্দ ছেড়ে নিজের দায়িত্ব পালন করলো, ছাড়া পাওয়া শব্দের সাথে সোর্সের আর কোনো কানেকশন থাকলো না।
ঠিক আছে বুঝলাম, তাহলে শব্দের বেগকে আসল বেগেই পাবো, এইতো?
হ্যাঁ, ঠিক তাই।
আমরা অবজারভারেরা শব্দের বেগ পাবো vᵥᵥ ।
১৩.
বেগ শব্দের বেগই, তাহলে সোর্সের গতির জন্য কি কিছুই চেঞ্জ হবে না?
হবে, অবশ্যই হবে।
আবারও সোর্স স্থির ধরে নিচ্ছি।
সোর্স থেকে শব্দের তরঙ্গের একটা চূড়া বের হলো। নির্দিষ্ট সময় পর আরেকটা চূড়া বের হয়ে 1 তরঙ্গদৈর্ঘ্য পুরো করবে। মানে ‘))’ পাবো। এই নির্দিষ্ট সময়টা কী?
পর্যায়কাল। আলোচিত শব্দ তরঙ্গের পর্যায়কাল ধরি
Tᵥᵥ ।
এখন সোর্স গতিশীল হলো।
আমাদের দিকে আসছে সোর্স। আর শব্দ তরঙ্গ তো সবসময় আমাদের দিকেই আসবে।
এখন একটু সোর্সের ওখানে জুম করে দেখতে হবে।
সোর্স প্রতি Tᵥᵥ সময় পরপর একটা করে ‘)’ বা চূড়া ছাড়ছে — আগেই দেখেছি। প্রথম ‘)’ ছাড়ার পর Tᵥᵥ সময় পরে সোর্স যখন দ্বিতীয় চূড়া ছেড়ে দিয়ে এক তরঙ্গদৈর্ঘ্য পুরো করতে যাবে, তখন কিন্তু সোর্স আর আগের (প্রথম চূড়া ছাড়ার জায়গায়) জায়গায় থাকবে না! কারণ এই Tᵥᵥ সময়ে সোর্সের নিজের বেগ vₛ এর জন্য কিছুটা এগিয়ে গেছে! শব্দ আর সোর্সের বেগের দিক এখানে একই। তাহলে ব্যাপারটা কী দাঁড়াচ্ছে?
হ্যাঁ, প্রথম চূড়াটা থেকে দ্বিতীয় চূড়াটার দূরত্ব কমে যাবে। কারণ ওই একটাই, সোর্স ‘)’ ছেড়ে আরেকটু সামনে এগিয়ে আরেকটা ‘)’ ছাড়বে। যেহেতু দুই চূড়ার দূরত্ব কমে গেছে, মানে তরঙ্গদৈর্ঘ্য কমেছে।
কমার পর কত পাচ্ছি, সেটা বের করা যাক।
সোর্স প্রথম চূড়াটা ছাড়লো। সেই চূড়াটা Tᵥᵥ সময় পর কত দূরত্ব সামনে যাবে?
বেগ = কম্পাংক × তরঙ্গদৈর্ঘ্য,
দূরত্ব মানে শব্দের আসল তরঙ্গদৈর্ঘ্য λᵥᵥ, আর সময় তো কম্পাংক, মানে fᵥᵥ = 1/Tᵥᵥ ।
তার মানে চূড়াটা যাবে,
vᵥᵥ = fᵥᵥ λᵥᵥ = λᵥᵥ/Tᵥᵥ
বা, λᵥᵥ = vᵥᵥTᵥᵥ
অর্থাৎ এই প্রথম চূড়াটা λᵥᵥ = vᵥᵥTᵥᵥ দূরত্ব অতিক্রম করার পর মানে এক তরঙ্গদৈর্ঘ্য অতিক্রম করার পরই তো দ্বিতীয় চূড়াটা সোর্স ছেড়ে দিবে। যে সময়টুকু লাগবে এই দূরত্ব অতিক্রম করতে, সেটা যেন কী?
পর্যায়কাল।
কিন্তু সোর্স তো দেখলামই– আগের জায়াগায় নেই। সোর্সের বেগের জন্য তো তাহলে সোর্সও এই পর্যায়কালের সময়টার মধ্যে আগের চেয়ে এগিয়ে যাবে। কতটুকু এগিয়ে যাবে?
s = vt
মান বসালে পাই, s = vₛTᵥᵥ , সোর্সের বেগ vₛ, আগেও বলেছি, আর সময়টুকু তো Tᵥᵥ, নতুন করে বলার নেই।
এবার খেয়াল করুন,
শব্দ আর সোর্স একই দিকে যাচ্ছে না? হ্যাঁ, তাই তো।
তাহলে নিশ্চই সোর্সের এগিয়ে গিয়ে দ্বিতীয় চূড়া ছাড়ায় প্রথম আর দ্বিতীয় চূড়ার মাঝের দূরত্ব কমে গেছে,
যেটুকু কমেছে, সেটা তো নিশ্চই Tᵥᵥ সময়ে, (প্রথম চূড়ার অতিক্রান্ত দূরত্ব – সোর্সের অতিক্রান্ত দূরত্ব) !!
মানে, নতুন করে দুই চূড়ার দূরত্ব ওরফে শব্দের তরঙ্গদৈর্ঘ্য পাবো,
⇨λᵥᵥ – s
= vᵥᵥTᵥᵥ – vₛTᵥᵥ
= Tᵥᵥ(vᵥᵥ – vₛ)
= (1/fᵥᵥ)(vᵥᵥ – vₛ)
= (vᵥᵥ – vₛ)/fᵥᵥ
আমরা পেয়ে গেলাম শব্দের নতুন তরঙ্গদৈর্ঘ্য।
আসলে সোর্স থেকে বের হওয়ার সাথে সাথেই এই তরঙ্গদৈর্ঘ্যের বিকৃতি ঘটছে, সোর্স যে গতিশীল তার জন্যে। শব্দটার আসল বৈশিষ্ট্য মানে প্রকৃত তরঙ্গদৈর্ঘ্য বা কম্পাংক পাবো যখন সোর্স স্থির থাকবে। গতিশীল হলেই চেঞ্জ হয়ে যাবে৷ কিন্তু বেগ তো সবসময় একই থাকবে। মজার ব্যাপারটা এখানেই। বেগ যেহেতু চেঞ্জ হচ্ছে না, মানে ধ্রুবক, যেখানে,
বেগ = তরঙ্গদৈর্ঘ্য × কম্পাংক
কিন্তু তরঙ্গদৈর্ঘ্য ঠিকই পরিবর্তন হচ্ছে। কিন্তু শুধু তরঙ্গদৈর্ঘ্য কমে বা বেড়ে গেলে তো বেগও কমবেশি বেড়ে বা কমে যাবে। আবার বেগ ধ্রুবকও। তাহলে কী হবে? বেগ ঠিক রাখতে কম্পাংক কমে বা বেড়ে যাবে।
কতটুকু কমবে বা বাড়বে, সেটাই দেখব।
সোর্স ছেড়ে দেওয়ার পর তরঙ্গের বেগ, vᵥᵥ ই হবে, আগেই দেখেছি। আর ছেড়ে দেওয়ার পর তরঙ্গদৈর্ঘ্য কী হবে সেটা তো এতক্ষণের বকবকে দেখলামই,
(vᵥᵥ – vₛ)/fᵥᵥ । ছেড়ে যাওয়ার পর কম্পাংকটা কী সেটা তো জানি না। আমরা শুধু সোর্স স্থির অবস্থায় পাওয়া কম্পাংক জানি, আর সেটা দিয়ে আমরা ছাড়ার পর তরঙ্গদৈর্ঘ্য কত সেটা বের করলাম। ধরি পরিবর্তিত কম্পাংক fₒ , o মানে অবজারভার বা আমরা যে কম্পাংক দেখতে পাবো সেটা।
যাইহোক, আবারও, বেগ v = fλ সূত্র টেনে পাই,
vᵥᵥ = fₒ × (vᵥᵥ – vₛ)/fᵥᵥ
বা, fₒ = fᵥᵥ [vᵥᵥ/(vᵥᵥ – vₛ)]
অর্থাৎ, আমরা যদি fᵥᵥ বা শব্দের আসল কম্পাংক জেনে ফেলি, তাহলে এর সাথে [vᵥᵥ/(vᵥᵥ – vₛ)] গুণ দিলেই পেয়ে যাচ্ছি অব্জার্ভ করা কম্পাংক!
এখানে দেখুন, [vᵥᵥ/(vᵥᵥ – vₛ)] তে (vᵥᵥ – vₛ) অংশটা কিন্তু নিশ্চই vᵥᵥ থেকে ছোটো।
তাহলে [vᵥᵥ/(vᵥᵥ – vₛ)] এর মানে দাঁড়াচ্ছে বড়ো কোনো সংখ্যাকে ছোটো সংখ্যা দিয়ে ভাগ। এবং অবশ্যই এই ভাগফল 1 থেকে বেশি।
ধরি, Γ = [vᵥᵥ/(vᵥᵥ – vₛ)]
তাহলে, fₒ = fᵥᵥ [vᵥᵥ/(vᵥᵥ – vₛ)]
বা, fₒ = fᵥᵥΓ, যেখানে Γ ≥ 1
তাই নিশ্চই fᵥᵥ থেকে fₒ বড়ো, মোটকথা, আসল কম্পাংক বা ফ্রিকুয়েন্সি থেকে অব্জার্ভ করা কম্পাংক বেশি হবে। আমরা শব্দ বেশি তীব্রভাবে শুনতে পাবো।
১৪.
এবার দ্বিতীয় কন্ডিশনে দেখা যাক।
না, না দেখেই বলে দিতে পারা যাবে কিন্তু!
সোর্স আমাদের থেকে দূরে সরে যাচ্ছে। তাই আমরা এখানে শব্দের নতুন তরঙ্গদৈর্ঘ্য বেশি পাবো।
একটু কল্পনা করি,
সোর্স প্রথম চূড়া ছেড়ে দেওয়ার পর সেই চূড়া থেকে কিছুটা দূরে সরে গিয়ে দ্বিতীয় চূড়া ছেড়ে দিলো।
দুই চূড়ার দূরত্ব বেড়ে গেল, তরঙ্গদৈর্ঘ্য বেড়ে গেল।
সমীকরণ বের করতে চাইলে নতুন তরঙ্গদৈর্ঘ্য পাবো,
vᵥᵥTᵥᵥ + vₛTᵥᵥ ,
আগের কন্ডিশনে ছিল
vᵥᵥTᵥᵥ – vₛTᵥᵥ
শুধু প্লাস-মাইনাস তফাত, আরকিছু না৷
তো বের করলে দ্বিতীয় কন্ডিশনের জন্য পাচ্ছি,
fₒ = fᵥᵥ [vᵥᵥ/(vᵥᵥ + vₛ)]
বোঝাই যাচ্ছে, fᵥᵥ এর চেয়ে fₒ ছোটো। মানে অব্জার্ভ করা কম্পাংক কম পাবো।
তাহলে একটা সমন্বিত সমীকরণ লিখতেই পারি,
fₒ = fᵥᵥ [vᵥᵥ/(vᵥᵥ ± vₛ)]
যখন সোর্স অবজারভারের কাছে আসছে, তখন মাইনাস আর যখন দূরে সরে যাচ্ছে, তখন প্লাস।
সিম্পল।
আজ এপর্যন্তই।
পরের পর্বে টাইপ-৩ নিয়ে আলোচনা হবে। এবারেও একটা মজার সমস্যা দিয়ে যাই। আচ্ছা, যেহেতু এই টাইপে আপেক্ষিক বেগ নেই, মানে তরঙ্গের বেগ সবসময়ই তরঙ্গের বেগের সমানই। তাহলে এই টাইপের তরঙ্গদৈর্ঘ্যের পরিবর্তন কি আলোর ক্ষেত্রেও সত্যি হবে?? আলোর ডপলার ইফেক্টে বা রেডশিফট/ব্লু শিফটে??
১৫.
টাইপ-৩:
সোর্স আর অবজারভার দুজনেই মুভ করছে।
এই ধরণে খুবই চমৎকার জিনিস ঘটে।
আমরা মোট চারটা কন্ডিশন পাবো। আগের দুইটা টাইপ-১ আর টাইপ-২ ব্যাখ্যা করার সময় যে সমীকরণ আর অবস্থা দেখেছি, এটাতে সেগুলোর সমন্বয় হবে!
টাইপ-১ এর দুইটা কন্ডিশন ছিল৷ দুটোতেই শুধু অবজারভার মুভ করছিল।
A 1. শব্দ তরঙ্গের মুখোমুখি, সমীকরণ: fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/vᵥᵥ]
A 2. শব্দের সাথে একই দিকে, মানে শব্দের সাথে দৌড় পাল্লা দিয়ে,
সমীকরণ: fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/vᵥᵥ]
টাইপ-২ এর ছিল দুটো, দুটোতেই শুধু সোর্স মুভ করছিল।
B 1. সোর্স আমাদের দিকে আসছে,
সমীকরণ: fₒ = fᵥᵥ [vᵥᵥ/(vᵥᵥ – vₛ)]
B 2. সোর্স আমাদের থেকে দূরে সরে যাচ্ছে,
সমীকরণ: fₒ = fᵥᵥ [vᵥᵥ/(vᵥᵥ + vₛ)]
তো এই টাপ-৩ এ এসে আমরা সোর্স আর অবজারভার দুটোকেই মুভ করতে দেখছি। এখন উপরের চারটা শর্তকে দুটো দুটো করে নিলে এরকম কন্ডিশন পাবো,
A. অবজারভার শব্দের বিপরীতে মুভ করছে, সোর্স আর অবজারভার একইদিকে,
B. অবজারভার শব্দের বিপরীতে মুভ করছে, সোর্সও অবজারভারের বিপরীতে,
C. অবজারভার শব্দের বেগের একইদিকে মুভ করছে, সোর্স আর অবজারভার একইদিকে,
D. অবজারভার শব্দের বেগের একইদিকে মুভ করছে, সোর্স অবজারভারের বিপরীতে।
তো চারটা কন্ডিশন একইচিত্রে দেখলে কেমন হবে, সেটা একটু দেখে নেই।
১৬.
কন্ডিশন চারটা,
চাররকমের সমীকরণ আসবে,
চাররমকের ঘটনা ঘটবে,
এত পেঁচিয়ে আমরা চলব না। আমরা আগেও খুব সহজ পথে হেঁটেছি, এখনও খুব সহজ পথ ধরেই হাঁটব।
আমরা আগে কন্ডিশন A এর জন্য দেখব।
শুধু A নিয়ে চিন্তা করব, তাই মূল চিত্রকে একটু সহজ করে ফেলি, A রেখে সব মুছে দেই,
এবার খেয়াল করি। না, এই অংশের জন্য আগের হাবিজাবি শর্ত, হ্যানত্যান কিচ্ছু মনে রাখা লাগবে না৷ কাজেও আসবে না এসব৷
চিত্র দেখেই সব চিন্তা করে ফেলতে পারি।
আমরা দেখছি,
অবজারভার শব্দের বিপরীতে মুভ করছে। শব্দের বিপরীতে মুভ করলে যেন কী হয়? ওইযে, জাস্ট কম্পাংক বাড়ে, মনে আছে? না থাকলেও চিত্র দেখে বুঝে গেছেন জানি। দুইটা চূড়ার মাঝের দূরত্ব অতিক্রম করছে শব্দ নিজে, আর অবজারভার মানে আমাদের বেগ। তাই দুই চূড়ার মাঝের দূরত্বের খানিকটা আমরা অতিক্রম করে শব্দের নতুন আরেকটা চূড়া কানে ধরে ফেলছি। তাহলে এক সেকেন্ডে বা যেকোনো নির্দিষ্ট সময়ের মাঝে আমরা আগের চেয়ে বেশি চূড়া কানে ধরে ফেলছি। তাই কম্পাংক বেড়েছে মনে হচ্ছে।
আচ্ছা, এখানে তো আবার সোর্সও শব্দের বিপরীতে যাচ্ছে, তাহলে যে তরঙ্গদৈর্ঘ্য বাড়ার কথা?
হ্যাঁ, বাড়বে।
তো এইযে বেড়ে গেল, এটা কি আমাদের পাওয়া বেড়ে যাওয়া কম্পাংককে প্রভাবিত করবে না?
করবে তো৷ এই প্রভাবিত করার জন্যই কিন্তু আমরা এখন এই কম্পাংক বা fₒ (o = অবজারভার) কত হবে
সেটা আমরা জানিনা। আর এটাই আমরা এখন নির্ণয় করতে যাব।
আমরা জাস্ট এটুকুই জানি এখন, যে সোর্স থেকে যে অবস্থায় তরঙ্গ আসছে, সেই তরঙ্গের উপরই আমরা কল্পনা করছি। আর তরঙ্গদৈর্ঘ্যের পরিবর্তন কিন্তু সোর্স শব্দ ছেড়ে দেওয়ার সময়ই করে দিয়েছে! তাই আমরা যখন কম্পাংক নিয়ে চিন্তা করছি, তখন আমরা সোর্সের বেগ বাদ দিতে পারি। আর সোর্সের বেগ বাদ দিয়ে নিলে আমরা কিন্তু একটাই তরঙ্গদৈর্ঘ্য পাচ্ছি, সেটা হচ্ছে সোর্স শব্দ ছাড়ার সময় যে মূল তরঙ্গদৈর্ঘ্য বিকৃত হয়েছে, সেটার বিকৃতরূপ। এই বিকৃতরূপই তো বাতাসে ছড়িয়ে পড়ছে, সোর্স থেকে, তাই না? তো এখন আমরা এই বিকৃতরূপকেই মূল তরঙ্গদৈর্ঘ্য বিবেচনা করব।
এতে কোনো সমস্যাই হবে না!
কারণ কম্পাংকের ব্যাপারটাতে জাস্ট বাতাসে পাওয়া তরঙ্গদৈর্ঘ্যই দরকার। যখন সোর্স স্থির ধরে অবজারভার গতিশীল ধরে করলাম, তখন কিন্তু সোর্সের থেকে আসা শব্দই বাতাসে পাওয়া শব্দের তরঙ্গদৈর্ঘ্য ছিল। কারণ তখন সোর্স থেকে অপরিবর্তিতভাবেই তরঙ্গ বাতাসে ছড়িয়ে পড়েছিল। এখানে শুধু বাতাসে পাওয়া তরঙ্গদৈর্ঘ্যই প্রধান।
তো, আপাতত সোর্স ডিএক্টিভ করে রাখি।
তাহলে আমরা ধরে নেই, সেই বিকৃত তরঙ্গদৈর্ঘ্য মানে আমাদের কল্পনা করা মূল তরঙ্গদৈর্ঘ্য λ ।
আর অবজারভার যেহেতু শব্দের বেগের বিপরীতে যাচ্ছে, মুখোমুখি গতি, তাই অবজারভার যে বেগ দেখবে, সেটা এই দুই বেগের যোগফল। টাইপ-১ দেখার সময় খুটিয়ে দেখেছিলাম ব্যাপারটা৷
তো, শব্দের বেগ হলো এখন, vᵥᵥ + vₒ
আর এই আপেক্ষিক বেগের জন্য যে তরঙ্গদৈর্ঘ্যে কোনো পরিবর্তন হয়না, কারণ আমরা সোর্স ধরছি না। ধরছি অবজারভার। তাই তরঙ্গদৈর্ঘ্য λই থেকে গেল।
আর কম্পাংক তো জানিই না, কম্পাংক নির্ণয়ের উপায়ই তো বের করব, তাই না?
তাহলে কম্পাংক ধরি, fₒ ।
তো, আমরা শব্দের বেগের সমীকরণ,
বেগ = কম্পাংক × তরঙ্গদৈর্ঘ্য
বা, কম্পাংক = বেগ/তরঙ্গদৈর্ঘ্য
বা, fₒ = (vᵥᵥ + vₒ)/λ ….. (1)
আচ্ছা।
এবার তাহলে আমরা সোর্সকে একটিভ করে দেই। তাহলে পাচ্ছি λ মানে বাতাসে পাওয়া তরঙ্গদৈর্ঘ্যের সাথে এক্কেবারে খাঁটি শব্দের তরঙ্গদৈর্ঘ্যের সম্পর্ক। খাঁটি মানে কোনোরকম বিকৃতি ছাড়া, বা সোর্সের স্থির অবস্থায় ছাড়া শব্দের তরঙ্গদৈর্ঘ্য।
তো এই সম্পর্কটা কিন্তু টাইপ-২ এ দেখেছিলাম।
বিকৃত তরঙ্গদৈর্ঘ্য হচ্ছে,
λ = vᵥᵥTᵥᵥ + vₛTᵥᵥ
= vᵥᵥ/fᵥᵥ + vₛ/fᵥᵥ
= (vᵥᵥ + vₛ)/fᵥᵥ
এবার এটা (1) এ বসিয়ে দেই,
fₒ = (vᵥᵥ + vₒ)/[(vᵥᵥ + vₛ)/fᵥᵥ]
= fᵥᵥ [(vᵥᵥ + vₒ)/(vᵥᵥ + vₛ)]
মানে, fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/(vᵥᵥ + vₛ)]
শেষ।
তো,
w = মূল তরঙ্গ
o = অবজার্ভার
s = সোর্স
আবার মনে করিয়ে দিলাম
১৭.
লক্ষণীয় একটা বিষয় আছে। এই অংশের পুরো মজাটা এখানে।
এখানকার টাইপ-১ আর টাইপ-২ এর এই ঘটনা দুটো দুইভাবে দেখুন৷ এভাবে,
যখন অবজারভার শব্দের মুখোমুখি যাচ্ছিল, তখন তো কম্পাংক বেড়ে যাচ্ছিল।
আবার যখন সোর্স শব্দের বিপরীতে যাচ্ছিল, তখন তরঙ্গদৈর্ঘ্য বেড়ে গিয়েছিল কিন্তু বেগ একই ছিল, ফলে বেগ = কম্পাংক×তরঙ্গদৈর্ঘ্য ঠিক রাখতে কম্পাংক বেড়ে গিয়েছিল।
মানে দুই ঘটনায়ই কম্পাংক বেড়েই গিয়েছিল। এবারে টাইপ-৩ এ এসে কন্ডিশন A তে এসে এই দুই ঘটনার সমন্বয় দেখলাম। কী পেলাম?
fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/(vᵥᵥ + vₛ)] এটা।
এখানে (vᵥᵥ + vₒ) তে মাঝে প্লাস আছে। এটা কিন্তু সেই টাইপ-১ এর ওই fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/vᵥᵥ] থেকে এসেছে, যেখানে স্পষ্ট কম্পাংক বেড়েছে বলেই মাঝে প্লাস এসেছে! আর এটা হয়েছে অবজারভারের বেগ থাকার জন্য। তাহলে একটা সিদ্ধান্তে আসা যেতেই পারে, যদি অবজারভারের বেগের কারণে কম্পাংক বাড়ে, তাহলে (vᵥᵥ + vₒ)/(vᵥᵥ + vₛ) এর উপরের পার্টে প্লাস চিহ্ন মাঝে হবে।
আবার নিচের (vᵥᵥ + vₛ) এরদিকে দেখলেও আপনি টাইপ-২ এর জন্য একই জিনিস— কম্পাংক বেড়ে যাওয়া দেখতে পাবেন। তার মানে, সোর্সের গতি যদি কম্পাংক বাড়ায় বলে, তাহলে নিচে প্লাস হবে।
মজার না?
তাহলে বলুন দেখি, বাকি কন্ডিশন কেমন হবে, যদি অংক না করেই সূত্র বলে দেই!!
সহকারী সূত্র:
আগেরটাই। আসলে সমীকরণ প্রতিপাদন সহজ করে ব্যাখ্যা করতেই এত বড়ো পোস্ট যে পর্ব করতে হচ্ছে!
১৮.
কন্ডিশন B এর জন্য চিন্তা করি।
এখানে অবজারভারের বেগের জন্য কম্পাংক বাড়ছে। অবজারভারের সাপেক্ষে। আর সোর্সের বেগের জন্য তরঙ্গদৈর্ঘ্য কমে যাচ্ছে।
তাহলে যদি আমরা সমীকরণ আনতে চাই, তবে,
অবজারভারের জন্য,
(vᵥᵥ + vₒ) বেগ, কম্পাংক, fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/vᵥᵥ]
আর তরঙ্গদৈর্ঘ্যটা হবে হচ্ছে, সোর্সের ছাড়ার পর কমে যাওয়া তরঙ্গদৈর্ঘ্য, মানে, (vᵥᵥ – vₛ)/fᵥᵥ
তাহলে এখন কম্পাংক = বেগ/তরঙ্গদৈর্ঘ্য থেকে পাই,
fₒ = (vᵥᵥ + vₒ)/[(vᵥᵥ – vₛ)/fᵥᵥ]
= fᵥᵥ [(vᵥᵥ + vₒ)/(vᵥᵥ – vₛ)]
অর্থাৎ, fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/(vᵥᵥ – vₛ)]
চিত্রতে আগেই দেখেছি, কম্পাংক বেড়েছে, তরঙ্গদৈর্ঘ্য কমেছে। কম্পাংক শুধুমাত্র অবজারভারের বেগের জন্যই বদলায়, তরঙ্গদৈর্ঘ্য শুধুমাত্র সোর্সের বেগের জন্য বদলায়। তাই এখানে (vᵥᵥ + vₒ) তে অবজারভারের বেগ যোগ হয়েছে, (vᵥᵥ – vₛ) তে সোর্সের তরঙ্গদৈর্ঘ্য কমেছে বলে সোর্সের বেগ বিয়োগ হয়েছে।
আমরা ইচ্ছে করলে এখন C, D এর জন্য অংক না করেই এভাবে বলে দিতে পারব।
১৮.
C চিত্র দেখি৷
এখানে অবজারভারের বেগ কম্পাংক কমাচ্ছে, সোর্সের বেগ তরঙ্গদৈর্ঘ্য কমাচ্ছে৷
তাই,
fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/(vᵥᵥ – vₛ)]
বিশ্বাস না হলে বের করে মিলিয়ে নিতে পারেন, A এর মতো।
আবার একই উপায়ে,
D এর জন্য চিত্র দেখি।
D তে অবজারভারের বেগ কম্পাংক কমাচ্ছে, সোর্সের বেগ তরঙ্গদৈর্ঘ্য বাড়াচ্ছে। তাহলে,
fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/(vᵥᵥ + vₛ)]
সিম্পল।
১৯.
আমাদের পাওয়া চারটা সমীকরণ হচ্ছে,
A এর জন্য fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/(vᵥᵥ + vₛ)]
B এর জন্য fₒ = fᵥᵥ [(vᵥᵥ + vₒ)/(vᵥᵥ – vₛ)]
C এর জন্য fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/(vᵥᵥ – vₛ)]
D এর জন্য fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/(vᵥᵥ + vₛ)]
আমরা এই চারটাকে এক করে সমন্বিত সমীকরণ লিখতে পারি। সেটা হবে,
fₒ = fᵥᵥ [(vᵥᵥ ± vₒ)/(vᵥᵥ ± vₛ)]
এখন নিশ্চয়ই মনে আছে, উপরের (vᵥᵥ ± vₒ) অংশটা হচ্ছে কম্পাংককে কেমন পাচ্ছি, সেটা। আর নিচের (vᵥᵥ ± vₛ) হচ্ছে তরঙ্গদৈর্ঘ্যকে কীভাবে পাচ্ছি সেটা।
দুটোর যেটা বাড়বে, সেটার মাঝে প্লাস হবে, কমলে মাইনাস।
যেমন, তরঙ্গদৈর্ঘ্য বাড়লে আর কম্পাংক কমলে,
fₒ = fᵥᵥ [(vᵥᵥ – vₒ)/(vᵥᵥ + vₛ)] হবে সমীকরণ।
এভাবে যত উপায়ে সাজানো যায়, সব সম্ভব৷
এরপরের পর্বে থাকবে অনেকগুলো মজার সমস্যা। দেখি, কয়টার সমাধান আসে, আর কয়টার আসে না । একটা সমস্যা আজই দিয়ে যাচ্ছি। দেখি সমাধান আসে কিনা!
২০.
এবার একটু সমস্যা দেই, এতক্ষণ যেটা নিয়ে আলোচনা করলাম আমরা, সেটার উপর ভিত্তি করে।
সমস্যা-১:
নাঈম ভাইয়া বক্কর ভাইকে তার গল্পগুলো থেকে বের করে দিয়েছেন। রাগে,শোকে বক্কর ভাই নাঈম ভাইয়ার গাড়ির পিছনে ছুটছে। নাঈম ভাইয়ার গাড়ি প্রতি সেকেন্ডে দশ মনিফ দূরত্ব অতিক্রম করছে। আর বক্কর ভাই দৌড়াচ্ছে এক মনিফ/সেকেন্ড। নাঈম ভাইয়া গাড়ির হর্ন বাজাচ্ছেন। হর্নের শব্দের কম্পাংক ছিল দশ হাজার হার্জ। এদিকে বক্কর ভাই নাঈম ভাইয়াকে ধরতেই পারছে না! অবশেষে নাঈম ভাইয়া বাড়িতে পৌছালেন। মোবাইল হাতে নিয়ে অবাক হয়ে গেলেন! আজকে নাকি ঢাকার তাপমাত্রা 37° সেলসিয়াস! তাও ভাইয়ার গরম লাগেনি! এই মুহুর্তে বক্কর ভাই বেল বাজালো। ভাইয়া গম্ভীর সূরে আওয়াজ করলো, “তুমি যদি আমার গাড়ির হর্নের তরঙ্গদৈর্ঘ্য বলতে পারো, তাহলে আমি তোমার কথা শুনব।”
বক্কর ভাই কিংকর্তব্যবিমুঢ় হয়ে জবাব দিলো। কিন্তু নাঈম ভাইয়া বলল যে হয়নি।
এখন আপনি কি পারবেন, বক্কর ভাই কী তরঙ্গদৈর্ঘ্য বলেছিল সেটা খুঁজে বের করতে? বক্কর ভাইকে নাঈম ভাইয়াকে রাজি করাতে কী করতে হবে মনে মনে করেন?
[এক মনিফ একক দূরত্ব = 293 পিপড়া লম্বালম্বি দাঁড়ালে যা হয় সেটা। বিসিবির অপরাজেয় কন্টেস্ট বিজেতা মনিফ শাহ্ চৌধুরী ভাইয়ের নামে এই এককের নামকরণ করা হয়, যার প্রবক্তা উনি নিজেই]
সহকারী সূত্র:
আগেরটাই। আসলে সমীকরণ প্রতিপাদন সহজ করে ব্যাখ্যা করতেই এত বড়ো পোস্ট যে পর্ব করতে হচ্ছে!
১.
রিলিটিভিস্টিক ডপলার ইফেক্ট।
নাম শুনেই কেমন যেন রিলিটিভিটি রিলিটিভিটি ভাব আসে। অনেকের আবার ভয় ভয় করবে৷ না, তেমন কোনো কাজের জন্য এর নাম রিলিটিভিস্টিক না। জাস্ট আলোর জন্য ডপলার ইফেক্ট, তাই।
আলো আসলেই রিলিটিভিটি শব্দটা জুড়ে বসে।
ক্লাসিক্যাল রিলিটিভিটির ডপলার ইফেক্ট।
এক, সোর্স আর অবজারভারের মাঝে আপেক্ষিক বেগ।
দুই, অবজারভারের বেগের জন্য তরঙ্গের বেগের পরিবর্তন হওয়া।
এইদুটো ছিল মূল।
কিন্তু থিওরি অব স্পেশাল রিলিটিভিটি আমাদের দেখিয়েছে আলোর বেগ আপেক্ষিক না৷ পরম। যে-কারো সাপেক্ষেই আলোর বেগ একই, c = 299,792,458 m/s । চাই সে যত বেগেই চলুক।
এই ব্যাপারটাই ক্লাসিকাল মেকানিক্সের ডপলার ইফেক্ট থেকে আলোর ডপলার ইফেক্টকে আলাদা করেছে। ক্লাসিকাল মেকানিক্সের মতো এখানে অবজারভারের বেগের জন্য আলোক তরঙ্গের বেগের তারতম্য হবে না।
c-ই থাকবে সবসময়।
তাহলে আমরা পাচ্ছি, রিলিটিভিস্টিক ডপলার ইফেক্ট বা আলোর জন্য ডপলার ইফেক্ট হওয়ার মাত্র একটা শর্তই টিকে যাচ্ছে। সেটা হচ্ছে সোর্স আর অবজারভারের মাঝে আপেক্ষিক বেগ।
আরও সিম্পল করে বলতে গেলে জাস্ট সোর্সের বেগ।
তাহলে অবজারভার যে বেগেই চলুক, তার দেখা আলোর উপর তার কোনো প্রভাব পড়বে না?
পড়বে। কিন্তু সেটা কাউন্ট করা হবে অবজারভারের বেগ হিসেবে না। সোর্সের বেগের হিসেবে৷
কেন?
আসছি।
২.
ক্ল্যাসিক্যাল মেকানিক্সের ডপলার ইফেক্টের কথা মনে আছে?
অবজারভারের বেগ যেন কেন কাউন্ট হয়েছিল?
অইযে, অবজারভারের বেগ শব্দের বেগকে যেন বাড়িয়ে দিচ্ছিলো, তাই না?
শব্দের বেগ vᵥᵥ, অবজারভারের বেগ vₒ হলে অবজারভার শব্দের বেগ পাবে,
vᵥᵥ ± vₒ । শব্দের বেগের দিকে গেলে মাইনাস, বিপরীতে গেলে প্লাস৷ এখন হিসেব করতাম এই বেড়ে যাওয়া বেগের জন্য পরিবর্তন হওয়া কম্পাংক।
তো এখন, আমরা জানি, আলোর এই আপেক্ষিক বেগটা হয় না। যেকোনো অবজারভার যেভাবেই চলুক, যেমন করেই থাকুক, আলোর বেগকে c-ই পাবে৷ মানে 299,792,458 এই সীমা অতিক্রম করবে না।
তাহলে আমরা বলতে পারি, অবজারভার যদি vₒ বেগেও চলে, তাও আলোর বেগ সে c ± vₒ না, বরং c-ই দেখবে৷ তাহলে এখানে বেগের পরিবর্তন নেই, মানে কম্পাংক সব একই। তরঙ্গদৈর্ঘ্যেরও পরিবর্তন নেই। সব ঠিকঠাক। এই অংশের ব্যাপারটা আর আলোর ডপলার ইফেক্ট ঘটাতে পারবে না।
৩.
ক্ল্যাসিক্যাল মেকানিক্সে আবার ফিরে যাই।
অবজারভার বাদ, আসি সোর্সে। সোর্সের বেগের জন্য তরঙ্গদৈর্ঘ্যের পরিবর্তন হচ্ছিল। সেটা কিন্তু আলো আর সোর্সের আপেক্ষিক বেগের জন্য না! বরং সোর্স এগিয়ে গিয়ে তরঙ্গের চূড়া ছাড়ত। তাই তরঙ্গদৈর্ঘ্য কমে বা বেড়ে যেত। মনে আছে?
তার মানে আমরা কিন্তু এইদিক দিয়ে ডপলার ইফেক্টকে আনতে পারি, আলোর জন্য।
কীভাবে? আসুন, দেখি৷
৪.
ডপলার ইফেক্ট কে দেখবে? অবশ্যই অবজারভার। সেই তো অব্জার্ভ করছে, নাকি?
তো অবজারভার যদি দেখে, তাহলে ধরুন আমরাই অবজারভার। আমরাই হিসেব-নিকেশ করব সব।
আমরা এখন স্থির। সামনে একটা আলোর সোর্স যাচ্ছে। বেগ তার vₛ । ভালো। আমরাও তো নিশ্চয়ই সোর্সের বেগ vₛ ই দেখব, তাই না? হুম।
গেল।
এবার আমরা যাচ্ছি vₒ বেগে। সোর্সও যাচ্ছে vₛ বেগে, আমাদের মুখোমুখি আসছে, মানে পরস্পর বিপরীতে।
তো আমরা তো সবসময়ই নিজেদের স্থিরই দেখি, তাই না, তো আমরা যত বেগেই যাই, নিজেরা নিজেদের স্থির মনে করি, আর বাকি সবকিছুকে গতিশীল মনে করি। এখানেও তাই। আমরা সোর্সের যে বেগ দেখব, সেটা হবে vₛ + vₒ বেগ। নিজেদের স্থির পাব।
আবার একইদিকে গেলে বেগ তখন মাঝে মাইনাস,
vₛ – vₒ । কারণ তো জানেনই, কল্পনা করলেই পাওয়া যায়।
আবার যেহেতু সোর্সের বেগের জন্যই ডপলার ইফেক্ট হচ্ছে, তো নিশ্চয়ই আমরা ডপলার ইফেক্টটাও পাব এই vₛ ± vₒ বেগেই। কারণ আমরাই অবজারভার। আর অবজারভারই ডপলার ইফেক্ট দেখবে, মানে আমরা যে বেগ দেখব, সেটাই কাউন্ট হবে। আমরাই রাজা!
এখন ধরুন, আমরা স্থির৷ মানে vₒ = 0, তাহলে কাউন্ট হওয়া বেগ, vₛ ± vₒ = vₛ , শুধু সোর্সের বেগ।
সাধারণভাবে লেখা যায়, v = vₛ ± vₒ । আমরা এখন কাউন্ট হওয়া বেগকে v বলব। v যা খুশি হবে৷ অবজারভারের বেগ যোগ হোক বা না হোক, কিন্তু সোর্সের বেগ থাকাই লাগবে। এটা শুন্য হলে জাস্ট অবজারভারের বেগই থাকে, কিন্তু অবজারভারের বেগ তো চলে না। তো আমরা পাচ্ছি v, v কখন থাকবে, সেটাও বুঝলাম।
এটুকু ক্লিয়ার?
৫.
এবার আসি আসল কথায়। বেগ আসলেই আসে টাইম ডাইলেশনের ব্যাপার, খুব ঝামেলা, তাই না?
মোটেও না।
আমরা অবজারভারেরা সোর্সের বেগ দেখব শুধু। তাই টাইম ডাইলেশন শুধু এই সোর্সের হবে বলেই দেখব। খেয়াল করুন, খুব মূল্যবান কথা বলা হয়েছে।
এর মানে কী?
এর মানে হচ্ছে—
আপনি যদি সোর্স হন, আর আমি যদি অবজারভার হই, তাহলে আপনি যদি আলোক তরঙ্গের পর্যায়কাল খেয়াল করেন, তাহলে পাবেন Tₛ । আমি দেখলে পাব Tₒ । কারণ আপনি, অবজারভার মানে আমার সাপেক্ষে গতিশীল। আপনার টাইম স্লো হয়ে গেছে আমার সাপেক্ষে। মানে আপনার দেখা পর্যায়কাল আর আমার দেখা পর্যায়কালের মাঝে সম্পর্ক,
Tₒ = TₛΓ
এখানে,
Γ = 1/√(1 – v²/c²)
জাস্ট টাইম ডাইলেশন। আরকিছুই না। ভয়ের কারণ নেই। ইজি।
৬.
এবার আমরা দেখি, যদি সোর্স আমাদের দিকে আসতে থাকে মানে সোর্স আর আলোক তরঙ্গ একইদিকের বেগ হয়, তাহলে কী হবে?
অবজারভার দেখবে, সোর্স এক তরঙ্গদৈর্ঘ্যের দুটি চূড়া ‘))’ এর ডানের চূড়া ছেড়ে দিলো। ঠিক এক পর্যায়কাল মানে Tₒ সময় পর দ্বিতীয় চূড়া ‘)’ ছাড়বে।
(এখন প্রশ্ন হচ্ছে এটা Tₛ হলো না কেন?
কারণ ব্যাপারটা পর্যবেক্ষণ করছে অবজারভার মানে আমরা)
কিন্তু এই Tₒ সময়ে সোর্সের বেগের জন্য সোর্স নিজেই সামনে এগিয়ে যাবে। এই সামনে এগিয়ে গিয়েই দ্বিতীয় চূড়াটা ছেড়ে দিবে। তাহলে দুই চূড়ার মাঝের ব্যবধান কমে যাবে। কতটুকু কমে যাবে, সেটা আগেও দেখেছি, ক্ল্যাসিক্যাল ডপলার ইফেক্ট দেখার সময়।
সেটা হচ্ছে, এই Tₒ সময়ে আলোর ডানের চূড়াটা যতদূরে গিয়েছে, বিয়োগ, Tₒ সময়ে সোর্স কতটুকু সামনে এগিয়েছে।
মানে, s = vt করে লিখতে পারি,
cTₒ – vTₒ
আর দুই চূড়ার মাঝখানের ব্যবধানই তো তরঙ্গদৈর্ঘ্য, তাহলে নিশ্চয়ই অবজারভারের দেখা তরঙ্গদৈর্ঘ্য হবে,
λₒ = cTₒ – vTₒ
এবার, বেগ = কম্পাংক × তরঙ্গদৈর্ঘ্য থেকে পাই,
λₒ = c/fₒ , fₒ হচ্ছে অবজারভারের দেখা কম্পাংক।
তাহলে,
λₒ = c/fₒ = λₒ = cTₒ – vTₒ
বা, c/fₒ = cTₒ – vTₒ
বা, c/fₒ = Tₒ(c – v)
আমরা আগে দেখেছি,
Tₒ = TₛΓ
এখানে,
Γ = 1/√(1 – v²/c²)
অর্থাৎ, c/fₒ = Tₒ(c – v)
= TₛΓ(c – v)
পর্যায়কাল = 1/কম্পাংক।
মানে, c/fₒ = TₛΓ(c – v)
= (1/fₛ)Γ(c – v)
এখন সমীকরণটাকে একটু নাড়াচাড়া দিই,
c/fₒ = TₛΓ(c – v)
= (1/fₛ)Γ(c – v)
মান বসিয়ে নিই,
cfₛ/fₒ = Γ(c – v)
= (c – v)/√(1 – v²/c²)
= (c – v)/√{(c² – v²)/c²}
বা, cfₛ/fₒ = c(c – v)/√(c² – v²)
বা, fₛ/fₒ = (c – v)/√(c² – v²)
= (c – v)/√{(c + v)(c – v)}
= √(c – v)/√(c + v)
তাহলে পাচ্ছি,
fₒ = fₛ √(c + v)/√(c – v)
এটাই সেই সমীকরণ।
রিলিটিভিস্টিক ডপলার ইফেক্টের সমীকরণ, যখন সোর্স অবজারভারের দিকে আসছে। এটাকে ব্লুশিফট বলা হয়৷ নক্ষত্র থেকে আসা আলো পর্যবেক্ষণের সময় মূল বর্ণালি থেকে আলোকে এই fₒ কম্পাংকে আলোর প্যাটার্ন পাওয়া যায়। fₒ বড়ো, আর fₛ ছোটো। বেশি কম্পাংক মানে বর্ণালির নীল রঙের সেটের দিকে, নীলের দিকে যত যাওয়া যায়, কম্পাংক তত বেশি পাওয়া যাবে। fₒ > fₛ, মানে নক্ষত্রের মূল বর্ণালির কম্পাংক fₛ এরচেয়ে fₒ বেশিই কম্পাংক বলছে। মানে ব্লু শিফট, নীলের দিকে সরে গেছে।
এখানে মজার ব্যাপার হচ্ছে, উপরে (c + v) কিন্তু এটাই বুঝাচ্ছে যে এখানে কম্পাংক বেড়ে যাবে।
আমরা ঠিক এটাই দেখেছিলাম ক্ল্যাসিক্যাল ডপলার দেখার সময়। অবজারভারের দিকে সোর্স চললে কম্পাংক বেড়ে যায়। সমীকরণটা এভাবেই মনে রাখা যায় যে, কম্পাংক যে বাড়বে, সেটা জানি আমরা। তো, √(c + v)/√(c – v) তে উপরে নিশ্চয়ই (c + v) বড়ো সংখ্যা, আর (c – v) ছোটো সংখ্যা। c যেহেতু একই। তাই নিশ্চয়ই কম্পাংক বেড়ে গেলে শিওর উপরে প্লাস হবে৷
তো যখন সোর্স অবজারভারের বিপরীত দিকে যাবে, তখন তো অবশ্যই বেগের দিকটা আগের বেগের বিপরীত দিকে হবে। মানে একটা মাইনাস চিহ্ন জাস্ট। তাহলেই হয়ে যাবে৷
মানে, এইযে আমরা বের করলাম অবজারভারের দিকে সোর্স আসছে, সেটার সূত্রে সোর্সের বেগ v মাইনাস করে দিলেই পেয়ে যাব সোর্স অবজারভার থেকে দূরে সরে যাওয়ার সময়কার ডপলার ইফেক্ট!
এমন,
fₒ = fₛ √{c + (–v)}/√{c – (–v)}
বা, fₒ = fₛ √(c – v)/√(c + v)
হ্যাঁ, এখন যদি আমরা উপরের প্রক্রিয়ায় আবার অবজারভারের বিপরীত দিকে বেগের জন্য ডপলার ইফেক্টের সমীকরণ বের করি, তাহলে এই
fₒ = fₛ √(c – v)/√(c + v) ই পাব৷ বিশ্বাস না হলে এখনই দেখুন।
এটাও আগের টেকনিক ব্যবহার করে মনে রাখা যায়। এই ব্যাপারটাকে বলে রেডশিফট। মূল বর্ণালির fₛ এখানে বড়ো। আর পরিবর্তিত বর্ণালিতে পাওয়া যায় fₒ, যেটা fₛ এরচেয়ে কম হবে৷ বর্ণালিতে লালের দিকের রঙের সেটে কম্পাংক আস্তে আস্তে কমে। কমলার চেয়ে লালের কম্পাংক কম৷ এভাবে৷ তাহলে এখানে বর্ণালির প্যাটার্ন পাচ্ছি লালের দিকে সরে যাওয়া।
মানে রেডশিফট।
আজকের পর্ব এপর্যন্তই।
একটা কুইজ দিয়ে যাই।
আচ্ছা, সবসময় তো আর একদম ঠিক ঠিক মান লাগে না। যেমন, এইযে উপরের √(c + v)/√(c – v) এই অংশটাই সবকিছু নির্ধারণ করে দিচ্ছে৷ এই √(c + v)/√(c – v) ইউজ করলে পাব সবচেয়ে নিখুঁত মান, v৷ যত বেশিই হোক বা কমই হোক।
আচ্ছা, আপনি কি পারবেন, এমন একটা সহজ-সরল সমীকরণ বানাতে, যেটা অল্প বেগের জন্য ভালো কাজ করে, কিন্তু v আলোর কাছাকাছি বেগ হলে কাজ করে না? দেখুন তো, √(c + v)/√(c – v) কে সহজ করে কিছু বানানো যায় কিনা!?
সহায়ক সূত্র:
http://spiff.rit.edu/classes/phys314/lectures/doppdoppler.h
৮.
আগের পর্বে একটা প্রশ্ন ছিল। সেটার সমাধান নিয়েই আজকের এই পর্ব।
আমরা মোট দুটি সমীকরণ পেয়েছি।
রেডশিফটের জন্য,
fₒ = fₛ √(c – v)/√(c + v)
ব্লু শিফটের জন্য পেয়েছি,
fₒ = fₛ √(c + v)/√(c – v)
এটা হচ্ছে কম্পাংকের জন্য৷ চাইলে আমরা তরঙ্গদৈর্ঘ্যের জন্যও বের করে ফেলতে পারি।
যেমন, fₒ/fₛ কে লেখা যায়, (c/λₒ)/(c/λₛ) = λₛ/λₒ
তো এই দুটো সমীকরণে fₒ/fₛ = λₛ/λₒ ব্যবহার পাওয়া এমনিতেই পাওয়া যায়।
তো রেডশিফট, ব্লু শিফটের জন্য সবচেয়ে নিখুঁত মান দিবে আমাদের এই দুটো সমীকরণ। একদম একিউরেট মান দিবে। চাই সোর্সের বেগ আলোর কাছাকাছি হোক, বা একদম শুন্যের কাছাকাছি। কিন্তু সব সময় আমাদের এই জটিল দেখতে সমীকরণ লাগে না। কারণ হচ্ছে কম বেগ। সোর্সের বেগ মোটামুটি আলোর বেগের অনেক কম হলে এই সমীকরণ ব্যবহার জটিলতা বাড়ানো ছাড়া কিছু করে না। এইকাজের জন্য আমরা সমীকরণটাকে একটু কেটেকুটে পিচ্চি বানিয়ে নিতেই পারি, কি বলেন?
হুম, সেদিকেই যাব আমরা।
৯.
ব্লুশিফটের জন্য আমরা জানি,
fₒ = fₛ √(c + v)/√(c – v)
এখানে একটু জটিল জটিল দেখতে ব্যাপার আছে, সেটা নিশ্চয়ই বুঝে গেছেন এতক্ষণে।
তো আমরা এই √(c + v)/√(c – v) কে একটু সহজ করে আনতে চাই৷
এর জন্য আগে উপরে-নিচে √c দিয়ে ভাগ করে নিই।
তাহলে পাচ্ছি,
√(1 + v/c) ÷ √(1 – v/c)
তো এটায় পাওয়ার উপরে নিয়ে এলে হচ্ছে,
(1 + v/c) ¹/² × (1 – v/c) ⁻¹/²
এখানে একটা মজার ব্যাপার আছে।
(1 + v/c) ¹/² কে অসীম পর্যন্ত বিস্তৃত করলে পাই,
(1 + v/c) ¹/²
= 1 + (½)(v/c) + {(½(½ – 1)/ 2!} (v/c)² + {(½(½ – 1)(½ – 2)/ 3!} (v/c)³ +....
আলোর বেগ c অনেক বেশি। এখানে পদগুলোতে ধীরে ধীরে c এর পাওয়ার বাড়বে৷ আবার c আছে হরে, নিচে৷ মানে বিশাল সংখ্যা দিয়ে ভাগ হতে চলেছে৷ মানে ভাগ করার পর সংখ্যাটা অনেক অনেক ছোটো হভে৷ আমরা যেহেতু আসন্ন মান চাই, তাই জটিলতা এড়াতে এইসব ক্ষুদ্রাতিক্ষুদ্র মান বাদ দিয়ে শুধু দুইটা পদ নিয়ে লিখতে পারি,
(1 + v/c)¹/² ≈ 1 + (½)(v/c) = 1 + v/(2c)
একই ভাবে,
(1 – v/c) ⁻¹/² ≈ 1 – (–½)(v/c) = 1 + v/(2c)
তো এবার মূল সমীকরণে ফিরে গিয়ে মান বসাই,
(1 + v/c)¹/² × (1 – v/c)⁻¹/²
= {1 + v/(2c)} {1 + v/(2c)}
এবার (a – b)² সূত্র করে পাই,
1 + v/c + v²/(4c²)
এখানে আবার v²/(4c²) খুব বেশি ছোটো। আগের মতোই, c² দিয়ে ভাগ। এই পদটাও আমরা ইগনোর করে লিখতে পারি,
1 + v/c
গেল।
ব্লু শিফটের সমীকরণে এটা বসাই,
fₒ = fₛ √(c + v)/√(c – v)
= fₛ (1 + v/c)
এখন,
fₒ/fₛ = (1 + v/c)
বা, v/c = fₒ/fₛ – 1
আমরা যদি তরঙ্গদৈর্ঘ্য দিয়ে লিখতে চাই, তাহলে,
v/c = λₛ/λₒ – 1 = (λₛ – λₒ)/λₒ
এখানে আমরা পেলাম এই v/c । v/c কে z লেখা হয়, z হচ্ছে শিফটের পরিমাণ।
কতটুকু শিফট হচ্ছে, না হচ্ছে৷
১০.
ব্লু শিফটের মতো রেডশিফটের সমীকরণ বের করলে পাব, v/c = (λₒ – λₛ)/λₒ
ব্লু শিফটে পেয়েছিলাম, v/c = (λₛ – λₒ)/λₒ
ব্লু শিফটে অবজারভার করা তরঙ্গদৈর্ঘ্য কম ছিল। তাই উপরে (λₛ – λₒ) মানে মূল তরঙ্গদৈর্ঘ্যের থেকে বাদ দিয়ে ধনাত্মক মান পাওয়া।
রেড শিফটের ক্ষেত্রেও আমরা লক্ষ করে দেখতে পারি যে উপরের (λₒ – λₛ) ধনাত্মক। মোটকথা আমরা এই অংশকে সাধারণভাবে Δλ লিখতে পারি।
তাহলে রেডশিফট/ব্লু শিফটের সমীকরণ পাচ্ছি,
v/c = Δλ/λₒ
আর কিচ্ছু না।
আমরা শুধু পর্বেক্ষণ করা বর্ণালি দেখব। সেটা দেখে বুঝতে পারব যে সেটা ব্লু নাকি রেড শিফট। তারপর কতটুকু তরঙ্গদৈর্ঘ্য সরে গেছে, সেটা হিসাব করেই বলে দিতে পারব যে নক্ষত্র বা আলোক উৎসটার বেগ কত।
১১.
আপনি যদি একটু চালাক হন, আর সাথে অলসও হন তাহলে একটা সহজ কাজ করেই ফেলতে পারেন।
যেমন, আপনি জাস্ট রেডশিফটের সমীকরণ জেনে নিলেন৷ এখন আপনি ব্লু শিফটও মাপতে পারবেন এই সমীকরণ দিয়েই৷ তো, রেডশিফটের সমীকরণ হিসেবে
v/c = (λₒ – λₛ)/λₒ হয়৷ এখন ব্লু শিফটের সময় তো আবার λₛ বড়ো। তাইলে (λₒ – λₛ) থেকে মাইনাস মান আসবে।
v/c এর মান মাইনাস আসবে। মাইনাস, রেডশিফটের সমীকরণে মাইনাস। এর মানে রেডশিফটের উলটা বা ব্লু শিফট৷ মাইনাস বাদ দিয়ে বেগ বের করে নিলেই ব্লু শিফটের বেগ পেয়ে যাব। আসলে বেগ ব্যাপার না। রেড শিফটের সমীকরণে মাইনাস আসলেই বুঝতে হবে সেটা ব্লু শিফট। আবার ব্লু শিফটের সমীকরণে মাইনাস এলে বুঝতে হবে সেটা রেড শিফট।
কত্ত আলস বুদ্ধি তাই না?
প্রত্যেকবারের মতো মজার সমস্যা দিয়ে শেষ করব এই পর্ব।
নাঈম ভাইয়া গল্প লিখছেন৷ গল্পে বক্কর ভাই আর আক্কাস আলী একই স্পেসশিপে দূরের একটা হলুদ নক্ষত্রের দিকে যাত্রা করতে চলেছে। নক্ষত্রটার মোটামুটি বেগ নেই বলেই মনে হচ্ছে তাদের কাছে।
এবার স্পেসশিপের ইঞ্জিন স্টার্ট করা হলো। বক্কর ভাই চালাচ্ছে। তো স্পেসশিপ যখন বক্কর ভাই চালাচ্ছিল তখন নক্ষত্রের রঙ নীল দেখাচ্ছিল। আক্কাসের আবার এই নীল রঙ ভাল্লাগেনা। ও বক্কর ভাইয়ের সাথে মারামারি করে নিজে স্পেসশিপ চালানোর জন্য বসে পড়ল। আক্কাস চালানোর সময় দেখল নক্ষত্রের রঙ বেগুনী।
আক্কাস আলী, বক্কর ভাইয়ের চেয়ে কত জোরে স্পেসশিপ চালিয়েছিল??
সহায়ক সূত্র:
http://spiff.rit.edu/classes/phys314/lectures/doppler/doppler.html
❝গ্র্যাভিটেশনাল রেডশিফট❞
১.
বল উপরে ওঠে। নিচে ফিরেও আসে। উপরে তুলতে আমাদের দিতে হয় বল, ধাক্কা, ঢিল।
নিচে নামাতে কিছুই করতে হয় না আমাদের।
আমরা সবাই জানি ব্যাপারটা আসলে গ্র্যাভিটি নামক একটা ফোর্স বা বলের জন্য।
কিন্তু কেন একটা নির্দিষ্ট সময় পরেই নিচে আসবে?
সাথে সাথেই নিচে আসে না কেন?
জনাব জ্যাক একদলা মাটি ছুড়ে দিলেন।
মাটির দলা গতি পেল, উপরে উঠছে। গ্র্যাভিটি মাটির দলাকে নিচের দিকে টানছে। একটা ইলাস্টিক স্টিং (সুতা) এর মতো। যেন স্ট্রিং দলার সাথে বাধা, দলা উপরে উঠছে, স্ট্রিং লম্বা হচ্ছে, দলার বেগ কমছে। একসময় স্ট্রিং লম্বা হতে হতে দলার আর বেগ থাকবে না। স্ট্রিং চেপে আসবে তখন, দলা এসে জ্যাকের মুখের উপর পড়বে।
এই স্ট্রিংটা আসলে কী?
ফোর্স, গ্র্যাভিটি।
২.
বেগ কেন কমবে?
বেগ কমা মানে গতিশক্তি কমা। নিউটনিয়ান মেকানিক্সে গতিশক্তিকে লেখা হয় এভাবে, ½ mv² । দলা উপরে ওঠার সময় নিচের দিকে একটা বল কাজ করছে, সেটা হচ্ছে গ্র্যাভিটি। গ্র্যাভিটি টানছে, বিভবশক্তি থাকছে, mgd
গ্র্যাভিটির টানে মাটির দলা গতিশক্তি হারাচ্ছে, ½ mv² কমছে, v কমছে।
বস্তু উপরে ওঠার সময় বেগ আস্তে আস্তে কমে গিয়ে একটা উচ্চতায় এসে 0 হয়ে যাচ্ছে। এরপরে বস্তু আবার নিচে নামতে থাকবে।
এখানে বেগ কমাটা মুখ্য না। গতিশক্তি কমছে, সেটার সাইড ইফেক্ট হিসেবে শক্তির সংরক্ষণশীলতানীতি মানতে গিয়ে বেগ কমছে। ভূমি ছাড়ার মুহুর্তে যে গতিশক্তি থাকবে, উপরে ওঠার প্রতিমুহূর্তের গতিশক্তি আর বিভবশক্তির সমষ্টি ততই হবে৷ এর পেছনের কারণটা হচ্ছে প্রতি মুহুর্তে গতিশক্তি ঠিক ততটাই কমছে, যতটুকু বিভবশক্তি টানছে। বিভবশক্তি ঋনাত্মক এখানে৷ অনেকে এটাকে বলে গতিশক্তি বিভবশক্তিতে রুপান্তরিত হচ্ছে৷
৩.
আলোর বেগ কখনো কমে না।
মাটি থেকে আকাশের দিকে আলো ছুড়লে সেটার বেগও কমবে না। কিন্তু গতিশক্তি ঠিকই কমবে। কেন? কেন কমবে? বিভবশক্তি নিচের দিকে কাজ করছে।
আলো বা ফোটনের গতিশক্তিকে কয়েকভাবে দেখানো যায়।
E = mc², m হচ্ছে আপেক্ষিক ভর,
আলোর তরঙ্গধর্ম অনুযায়ী,
E = hf
এইদুটো মিলিয়ে লিখলে,
m = hf/c²
আলোর কণা ফোটনের স্থির অবস্থায় কোনো ভর নেই। রেস্ট ম্যাস জিরো। যখন গতিশীল থাকে, তখন আসে আপেক্ষিক ভর৷ সেটা হয় হচ্ছে, E = mc² অনুযায়ী, যেখানে m হচ্ছে সেই গতির জন্য বেড়ে যাওয়া ভরটুকু। এই ভরের জন্যই ফোটনকে গ্র্যাভিটি টানে, উপরে উঠতে গতিশক্তি কমে।
৪.
ধরা যাক এই মূহুর্তে আলোকে উপরে পাঠানো হলো।
নিচে থাকা অবস্থায় ধরি মোট শক্তি বা ফোটনের গতিশক্তি ছিল hf, বিভবশক্তি শুন্য। (যেহেতু d = 0)
উপরে উঠছে, গতিশক্তি তখন কম হবে, ধরি একটা বিন্দুতে গিয়ে গতিশক্তি হয়েছে hf' । যেহেতু গতিশক্তি কমবে, আর এখানে h বা প্ল্যাংক ধ্রুবক, তাই কম্পাংক f কেই বদলাতে হচ্ছে৷
আবার ওই মুহুর্তেই, ওই বিন্দুতে বিভবশক্তি হচ্ছে mgd.
তাহলে শক্তির সংরক্ষণশীলতানীতি থেকে পাই,
প্রথম দিকের বিভবশক্তি + প্রথমদিকের গতিশক্তি = পরবর্তী সময়ের বিভবশক্তি + সেই সময়ের গতিশক্তি
বা, 0 + hf = mgd + hf'
বা, hf = gd·hf/c² + hf' [যেহেতু, m = hf/c²]
বা, hf' = hf – gd·hf/c²
বা, hf' = hf (1 – gd/c²)
বা, f' = f(1 – gd/c²)
এখানে f' থেকে আমরা পাচ্ছি পরিবর্তিত কম্পাংক।
কিন্তু একটা প্রশ্ন থেকেই যাচ্ছে। এখানে h কী?
h হচ্ছে আমরা যে সীমার ভিতরে আলোর ভ্রমণের জন্য রেডশিফট হিসাব করছি।
আমরা যদি দেখতে চাই যে সূর্যের পৃষ্ঠ থেকে 100 মিটার উপরে ওঠার পর আলোর কম্পাংক কতটুকু চেঞ্জ হলো, তাহলে এই d = 100 m হবে৷
সোর্স:
Writer: Ashraful Islam Mahi